Lab 0: Sensor Calibrations

The first lab of the semester taught us an important lesson:
Don’t blindly trust all the data!
The main focus of the lab was to calibrate the telemetry devices Dr. Yim had made in-house, which had a 3-axis accelerometer and gyro, a thermistor, and a pressure sensor. We did this by putting the device in controlled states (i.e., taping it to a lathe turning at a fixed slow speed) and seeing what the appropriate reading (angular velocity along a particular axis) was. We then used a simple linear model for gain and offset to find actual values from what we sensed.

A calibration graph for angular velocity obtained by taping the sensor to a lathe in Penn's Precision Machining Laboratory. We aligned the sensor's x axis with the axis of rotation.

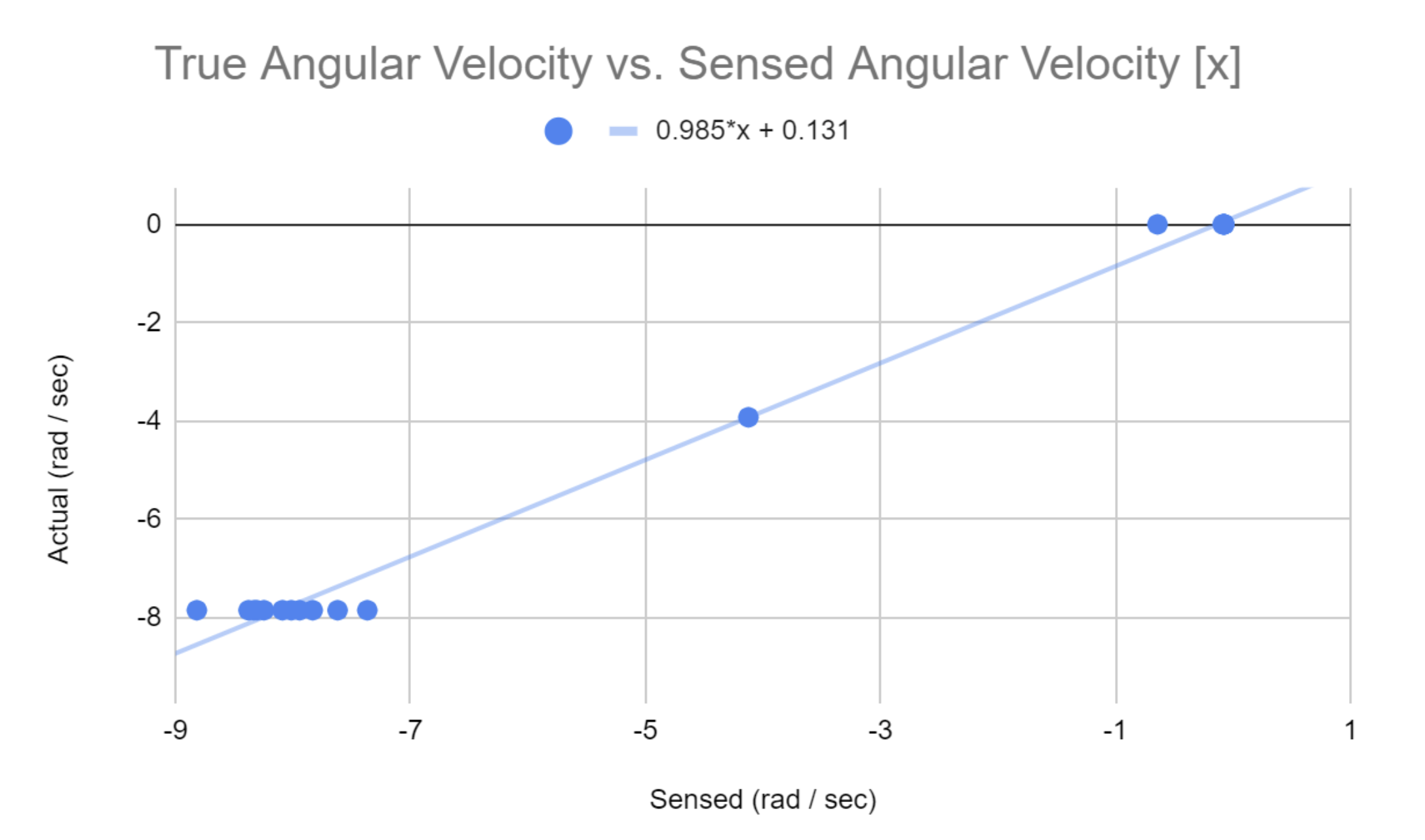
Report is here.

Lab 1: Heat Engine Optimization

Our second lab focused on maximizing power output on a heat engine by switching the air “tanks” between hot and cold baths. The expansion and contraction of gas would drive the engine. This would then lift a weight, which allowed us to measure the power output.

We used the fundamental relationships of the Ideal Gas Law to figure out how to optimize performance. For example, we recognized that filling the air tank while it was submerged in cold water would cause more air to enter the tank, which would result in a more powerful expansion stroke. Using a PV diagram and some simple calculations, we were also able to accurately estimate the power output of our system, which ended up being the highest in our lab section.

Derivation of formula for power output.

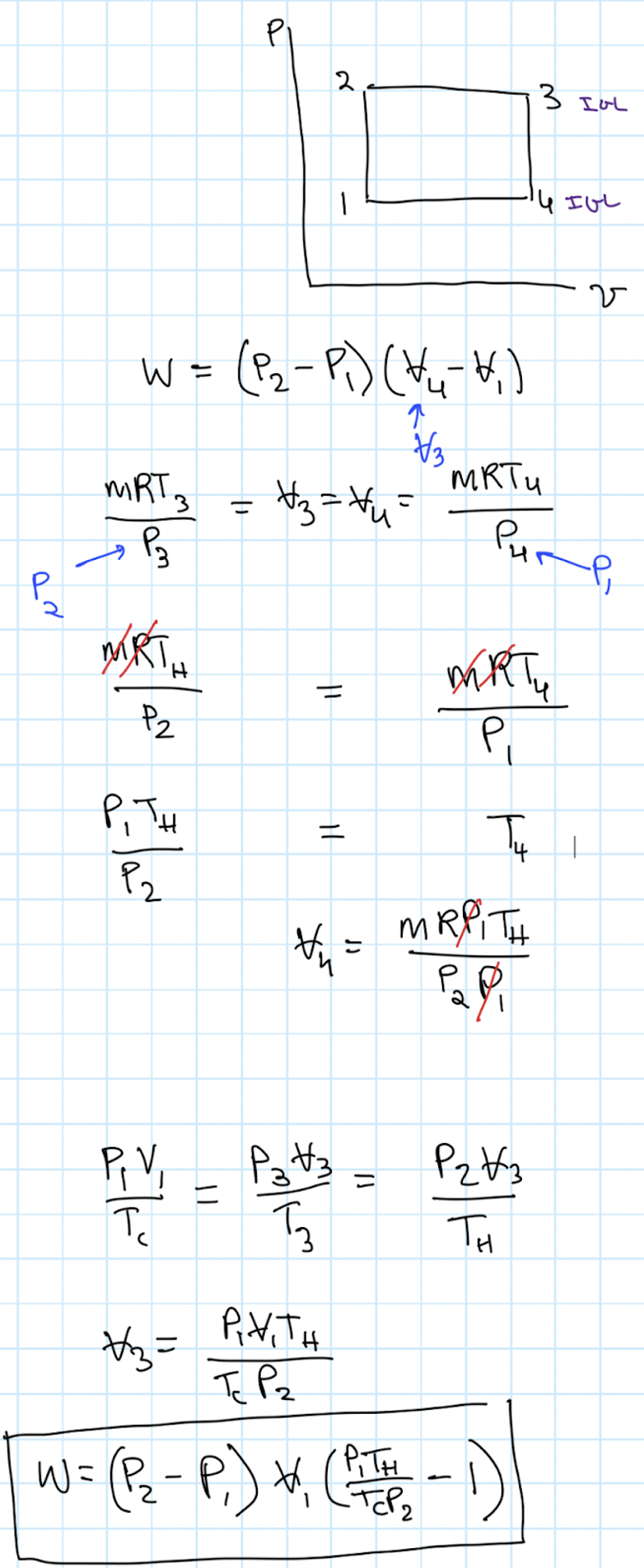
Report is here.

Lab 2: Ball Launcher

The goal of this lab was to launch a plastic ball from ground level, through a window, and hit a target on the ground on the other side. This involved:

Making a MATLAB solver to generate valid launch speeds and angles for inputted window and target locations
Designing and fabricating our launcher
Testing and revising our model (i.e., incorporating drag, introducing fudge factors…)

Our final launcher was made using laser-cut acrylic and a hefty amount of rubberbands. Below is the demonstration that scored us the most points. Our model wasn’t accurate enough to have it hit the correct targets, but it could pack a solid punch.

Lab 2 demonstration

Report is here.

Final Project: Butane Bottle Rocket!

Report is here.